shift-registers-0880cba7-8e70-4684-aff0-b3d7c3b16bf6

SHIFT REGISTERS

Shift registers are sequential binary circuits that may include feedback or operate without it, playing a crucial role in a variety of applications. These applications range from secure and restricted-access code generators to efficient code generators and even extend to mathematical modelling. In this discussion, I will concentrate specifically on random bit generators, finite state machines, and Markov processes, exploring their functions and significance in greater detail.

A pseudo-random bit generator can be created using a linear shift register sequence, where the probability of generating a particular sequence of m bits is $2^{-m}$$2^{-m}$2^(-m)2^{-m}$2^{-m}$, provided that the length of the sequence m is less than n bits. This method allows for the production of sequences that appear random, even though they are generated through a deterministic process.

A shift register operates as a finite state machine characterized by cycles that do not diverge, ensuring that the device retains information without any loss. This means that the sequence of states follows a fixed path without any branching, allowing for reliable preservation of data. Additionally, a binary Markov process can be represented using a shift register that cycles back to its initial state after completing p state transitions, effectively modeling the probabilistic behavior of the process within a finite loop.

SHIFT REGISTERS AND FINITE MACHINES

A finite state machine (FSM) is a device with a set of states $S=\{s_i\}$$S=\{s_i\}$S={s_(i)}S = \{s_i\}$S=\{s_i\}$ that can accept inputs $A=\{a_i\}$$A=\{a_i\}$A={a_(i)}A = \{a_i\}$A=\{a_i\}$ and produce outputs $B=\{b_i\}$$B=\{b_i\}$B={b_(i)}B = \{b_i\}$B=\{b_i\}$. Additionally, there is a function $\mu (s_i,a_i)$$\mu (s_i,a_i)$mu(s_(i),a_(i))\mu(s_i, a_i)$\mu (s_i,a_i)$ that determines the output based on a specific input and state, and a function $\delta (s_i,a_i)=s_{i+1}$$\delta (s_i,a_i)=s_{i+1}$delta(s_(i),a_(i))=s_(i+1)\delta(s_i, a_i) = s_{i+1}$\delta (s_i,a_i)=s_{i+1}$ that defines the transition to the next state.

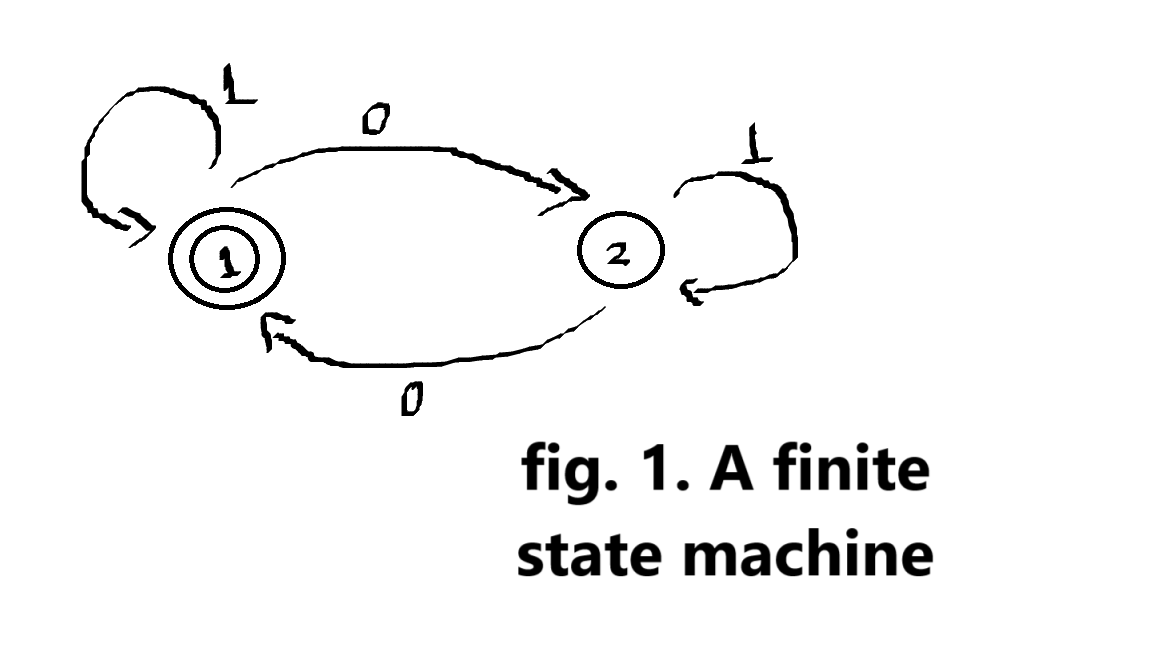
The functioning of a finite state machine can be demonstrated through a function table as presented below:

Table 3 illustrates a Finite State Machine with input set $A=\{0,1\}$$A=\{0,1\}$A={0,1}A = \{0,1\}$A=\{0,1\}$, state set $S=\{R,S,T\}$$S=\{R,S,T\}$S={R,S,T}S = \{R, S, T\}$S=\{R,S,T\}$, and output set $B=\{\alpha ,\beta ,\gamma \}$$B=\{\alpha ,\beta ,\gamma \}$B={alpha,beta,gamma}B = \{\alpha, \beta, \gamma\}$B=\{\alpha ,\beta ,\gamma \}$.

Beginning in state R, when the input string 100101 is processed, the machine generates the output β and concludes in state T, which is designated as the "terminal" state.

Two machines are considered equivalent if they produce identical output sequences for the same input sequences. In other words, their transformations are identical. Equivalence plays a crucial role in simplifying a circuit or a larger machine.